- Услуги
- Цена и срок
- О компании
- Контакты
- Способы оплаты
- Гарантии
- Отзывы
- Вакансии
- Блог
- Справочник
- Заказать консультацию
Заказать консультацию
Расчет обобщающих параметров непрерывных рент
Во всех рассмотренных выше рентах предполагалось, что члены потока платежей поступают дискретно — через фиксированные интервалы времени. Вместе с тем иногда более адекватное описание потока платежей достигается, когда он воспринимается как непрерывный процесс. Например, когда отдача от инвестиций происходит так часто, что в целом этот поток можно рассматривать как непрерывный. Предположение о непрерывности в определенных условиях увеличивает возможности количественного анализа, особенно анализа сложных схем долгосрочных производственных инвестиций.
Постоянная непрерывная рента. Приведем формулы для расчета современной стоимости и наращенной суммы постоянной непрерывной ренты при условии, что применяется годовая дискретная процентная ставка. Найдем коэффициент приведения такой ренты, обозначим его . Очевидно, что искомый показатель является пределом коэффициента приведения р-срочной ренты при. Получим:

В свою очередь, коэффициент наращения непрерывной ренты имеет вид:
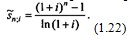
Переход от дискретных взносов постнумерандо к непрерывным увеличивает соответствующие обобщающие показатели и коэффициенты приведения и наращения рент в i/ln(1 + i) раз:

Пример 9. Ожидается, что доходы от эксплуатации месторождения полезных ископаемых составят 1 млрд. руб. в год, продолжительность разработки — 10 лет, отгрузка и реализация продукции непрерывны и равномерны. Капитализированная стоимость дохода при дисконтировании по ставке 10% составит:
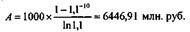
Важно отметить, что равномерная и непрерывная выплата годовой суммы примерно равнозначна (по влиянию на величины А и S) разовой выплате этой суммы в середине года. Иначе говоря, замена непрерывной постоянной ренты на более привычную дискретную с отнесением платежей к середине периодов мало повлияет на результаты расчетов. Обобщающие параметры ренты в этом случае рассчитываются по формулам, полученным для дискретных рент с учетом множителя (1 + i)1/2.
Пример 10. Заменим в примере 9 непрерывную ренту на дискретную с отнесением членов ренты к серединам годовых интервалов. В этом случае
A = 1000а10;10 х 1,11/2 = 1000 х 6,14457 х1,10,5 = 6444,48 млн. руб.
Расхождение с точным ответом обнаруживается только в четвертой цифре.
Заметим, что формулы (1.21), (1.22) предполагают непрерывное поступление платежей и дискретное начисление процентов.
Вероятно, более “естественным” является положение, когда оба процесса рассматриваются как непрерывные, т. е. поступления платежей и начисления процента происходят в бесконечно малые отрезки времени.
Чтобы методы работы с рентами, предусматривающими непрерывное начисление процентов, были более понятными, напомним, как начисляются непрерывные проценты. Формулы наращения и дисконтирования в этом случае записываются следующим образом:
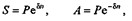
где — ставка непрерывных процентов (force of interest). В русской финансовой литературе эта величина получила название сила роста;
е — основание натуральных логарифмов.
Между дискретными и непрерывными ставками, как известно, существуют зависимости, позволяющие определить эквивалентные размеры ставок, т. е. ставок, дающих одинаковые финансовые результаты:
Из выражения (1.24) следует
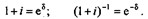
Перепишем теперь формулы (1.21) и (1.22), использовав эти соотношения. Получим
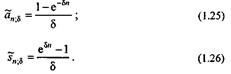
Формулы (1.21), (1.22) и (1.25), (1.26) дают тождественные результаты только в том случае, когда непрерывные и дискретные ставки являются эквивалентными.
Пример 11. Пусть в примере 9 дисконтирование осуществляется по силе роста, равной 10%, тогда, используя (1.25), получим 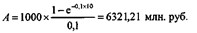
Сила роста, эквивалентная дискретной ставке 10%, составит: ![]() , или 9,531%. Откуда
, или 9,531%. Откуда 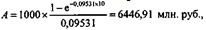
т. е. получен тот же результат, что и в примере 9.
Если поток платежей непрерывен и описывается функцией rt = f(t), то общая сумма поступлений за время п равна ![]()
В этом случае современная стоимость и наращенная сумма (при начислении процентов используется процентная ставка в виде силы роста) находятся как
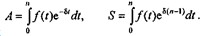
Причем зависимость между А и S можно представить как
![]()
Чтобы рассчитать величины А и S, необходимо определить конкретный вид функции изменения платежей и значения ее параметров. Рассмотрим методы расчета современных стоимостей только для двух видов функций — линейной и экспоненциальной.
Линейно изменяющийся непрерывный поток платежей. Функция такого потока
Rt =R0+at,
где R0 — начальный размер платежа, выплачиваемого в единицу времени, в котором измеряется срок ренты;
а — прирост в единицу времени.
Современная стоимость получена с помощью интегрирования функции потока платежей:
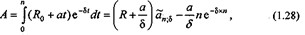
где an;b— коэффициент приведения постоянной непрерывной ренты (см. (1.25)).
Пример 12. Намечается ежегодно в течение трех лет увеличивать выпуск продукции на 1 млрд. руб. Базовый уровень выпуска — 10 млрд. руб. Необходимо определить суммарный стоимостной объем выпуска с начислением процентов — сила роста 8%.
Сначала определим современную стоимость данного непрерывного потока поступлений (см. (1.28)):

Коэффициент приведения составит: 
Таким образом, А = 30,512 млн. руб.
Затем на основе (1.27) находим наращенную сумму:

Чтобы методика определения современной стоимости непрерывной ренты была более наглядной, решим поставленную задачу иным способом, предварительно трансформировав непрерывную ренту в дискретную с платежами в середине периодов. Получим такую последовательность: 10,5; 11,5; 12,5. Затем определим процентную ставку, эквивалентную силе роста 0,08. Находим
i = е0,08-1=0,083287.
Искомая величина составит:
А = 10,5 х 1,08329-0,5 + 11,5 х l,08329-1,5 + 12,5 х 1,08329-2,5 = = 30,522.
Как видим, погрешность незначительна.
Экспоненциальный рост платежей. Поток платежей описывается экспоненциальной функцией
Rt = R х еgt.
Назовем параметр g непрерывным темпом прироста платежей. Между принятым в статистике дискретным темпом прироста k и непрерывным существует следующая зависимость:
g = ln(l + k).
Современная величина такой ренты находится следующим образом:

В знаменателе формулы (1.29) фигурирует разность параметров, характеризующих непрерывные процессы. Эту разность легко найти с помощью дискретных параметров роста платежей и начисления процентов, которые обычно и задаются в условиях формирования потока платежей, а именно
![]()
Пример 13. Ожидается, что прирост доходов на протяжении трех лет составит 5% в год (k = 0,05). Какова современная стоимость и наращенная сумма потока доходов, если R = 100, i = 7%, п = 3 года?
Из условий задачи следует:
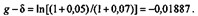
Таким образом, на основе (1.29) получим:
Статьи по теме
- Методы определения интервальных прогнозов
- Основные элементы методики
- Факторы, влияющие на размеры лизинговых платежей
- Методы расчета регулярных лизинговых платежей
- Схемы погашения задолженности по лизинговому контракту
- Финансовый и оперативный лизинг
- Анализ отзывчивости
- Моделирование инвестиционного процесса
- Дополнительные измерители эффективности
Полезные статьи









Узнайте цену услуг:
Узнай цену консультации
"Да забей ты на эти
дипломы и экзамены!”
(дворник Кузьмич)

